Transfer Staff (ASTOM): Sun Zhi-Gang Article List>> FEM Numerical Simulation of Retinal Detachment Surgery for Clinical Treatment Support 1. Research Purpose Retinal detachment is an important ophthalmologic condition that causes visual defect and occurs frequently in the eyeball, which is the only sensory organ in the human body that can receive external visual information. In clinical ophthalmology, several types of surgeries can be performed depending on the type of retinal detachment. Among them, scleral buckling surgery, which includes segmental and/or encircling buckling, is a representative surgical strategy for treating rhegmatogenous retinal detachment by suturing the buckling material on the sclera to buckle it for the reinstatement of the detached retina [1] (Fig. 1); a substantial number of surgeries are performed every year. However, the fundamentals of this surgery, such as the conformation and the installation position of the buckling material, the determination of the suture width, and the control of the intraocular pressure that fluctuates during the surgery, solely depend on the surgeon’s longstanding experience and intuitionin the actual clinical situation. Thus, it cannot be factually stated that the success rate of the surgery and its outcomes have been satisfactory. The buckling surgery simulator supported by FEM numerical simulation technology based on biomechanics is highly promising as a powerful tool to overcome the current problems. We conducted this research aiming at the realization of the simulator. The eventual goal of this study was to preliminarily simulate the clinical surgical procedure, and the appropriate surgical conditions were derived based on the mechanical information obtained from the simulator. Thus, we hope to accomplish a reduction in the cost to the patients, healthcare expenditure, and social contribution and to realize high-quality surgeries and highly advanced medical treatments. Fig. 1 (Please click the figure to enlarge it.) 2. Development of FEM Numerical Simulation Program It is evident that the development of numerical simulation program is the key to achieve the abovementioned goal. Although the buckling procedure may be perceived as an easily comprehensible mechanical phenomenon at the first glance, the faithful and accurate simulation of this procedure is extremely difficult. This is because the surgery targets the eyeball that consists of several soft tissues, including filamentous zonula ciliaris, and fluids with nonlinear mechanical properties, and there are frequent interactions among the soft tissues, buckling materials, soft tissues and buckling materials, or suture threads and buckling materials during the complex surgery. Therefore, as a target of the FEM numerical simulation, the surgical procedure is an extremely difficult case with various problems such as material, geometrical, and contact nonlinearities in addition to the requirement of solid-liquid coupling analysis and the analyses of the buckling and suturing procedures. Numerous researches have applied FEM numerical simulation for the analysis of biological organs or soft tissues [2]–[6], while there are only a few reports on its use for eyeball analyses [7], [8]. Particularly, there has been no research or program targeting the complex eyeball buckling surgery. Accordingly, we started with the 2D simulation (→Reference List (5), (6), (9), (10), and (12)), and overcame all the problems and independently developed the 3D FEM program that enables the simulation of the complex surgical procedure (→Reference List (7), (9), (13), (14), (18), and (19)). The functions of the program are as follows. 1) Extensive deformation of an incompressible hyperelastic body and analysis of nonlinear mechanical responses • Element type: 8/1 node hexahedral hybrid element • Boundary condition: Node displacement, node force, and surface pressure • Material model: 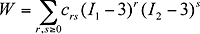2) Coupled analysis of the incompressible hyperelastic body and the quiescent fluid 3) Contact analysis between deformable bodies 4) Contact analysis between a soft body and a rigid body 5) Process analysis of eyeball buckling 6) Process analysis of suturing 7) Dialog-style input of buckling material model 8) Automatic generation of suture thread by selecting suture width, etc. 3. Example of Numerical Simulation Here, the simulation examples of the partial and circular buckling procedures are introduced. Simulation models and their results used for each example are shown in Figs. 2 and 4 and Figs. 3 and 5, respectively. The simulation was conducted by following the steps mentioned below. • Analysis of the application of the surface pressure boundary conditions within the eyeball to generate the standard intraocular pressure • Coupled solid-liquid analysis of eyeball buckling by using a silicon band (only for the circular buckling procedure) • Coupled solid-liquid analysis of buckling material suturing on the eyeball surface (Please click the figure to enlarge it.) Fig. 2 Fig. 3 Fig. 4 Fig. 5 Fig. 6 As seen in Figs. 3 and 5, the complex surgical procedure could be thoroughly simulated. In addition, the scleral buckling effect, the deformation of eyeball conformation with regard to parameters such as the eyeball length, the change in the volume of the subretinal fluid, the conditions and stress distributions of retinal reattachment and closure of retinal tear, and the information of the change in the intraocular pressure can be rationally comprehended by conducting the simulation. The comparison of the simulation results under different surgical conditions is demonstrated in Fig. 6. Information that provides guidelines for clinical surgeries can be obtained from the comparison. Followings are the examples: • A strong scleral buckling effect can be obtained when the protruded type silicon tire is used. • The retina reinstated by the circular buckling procedure that tightly fastens the retina, is strongly supported by the crystalline lens inside the eye (the relatively large compression of the crystalline lens by the buckling is revealed by the stress distribution of hydrostatic pressure). • The surgery causes an increase in the intraocular pressure. In particular, in the case of the circular buckling procedure that strongly tightens the eyeball, the intraocular pressure is significantly increased. As seen in the abovementioned simulation example, the program enabled the thorough and intact simulation of the complex buckling surgery and the acquisition of valuable information to be applied during a clinical surgery. By preliminarily simulating the surgical procedure with the consideration of various actual surgical conditions, the realization of clinical treatment support by using the numerical simulation is highly promising. Furthermore, since the program possesses various functions, it is expected that it can be used not only for the eyeball buckling procedure but also for the other applications. [1] ***** [2] Delfino, A. et al., J. Biomechanics , 30-8 (1997), 777-786. [3] Hirokawa, S. and Tsuruno, R., Med. Eng. Phys., 19-7 (1997), 637-651. [4] Natali, A. N., J..Biomed. Eng. , 13 (1991), 163-167. [5] Miller, K. et al., J. Biomechanics, 33-11 (2000), 1369-1376. [6] Bischoff, J. E. et al., J. Biomechanics, 33-6 (2000), 645-652. [7] *****, IOL&RS, 13(1999), 2-6. [8] Stitzel, J. D. et al., IV World Congress of Biomechanics(2002).